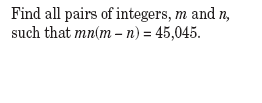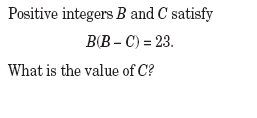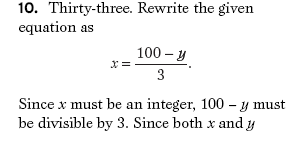|
Add the two equations.
 . .
Now, this can be rearranged:

and factored:

 , ,  , and , and  are all integers, so the three terms on the left side of the equation must all be perfect squares. Recognize that are all integers, so the three terms on the left side of the equation must all be perfect squares. Recognize that  . .
 , since , since  is the biggest difference. It is impossible to determine by inspection whether is the biggest difference. It is impossible to determine by inspection whether  or or  , or whether , or whether  or or  . .
We want to solve for  , so take the two cases and solve them each for an expression in terms of , so take the two cases and solve them each for an expression in terms of  . Our two cases are . Our two cases are  or or  . Plug these values into one of the original equations to see if we can get an integer for . Plug these values into one of the original equations to see if we can get an integer for  . .
 , after some algebra, simplifies to , after some algebra, simplifies to
 . 2021 is not divisible by 7, so . 2021 is not divisible by 7, so  is not an integer. is not an integer.
The other case gives  , which simplifies to , which simplifies to  . Thus, . Thus,  and the answer is and the answer is  . .
|